차원 축소는 고차원 데이터를 저차원으로 변환하여, 데이터를 처리하고 해석하기 쉽게 만드는 기법입니다. 이는 데이터의 복잡성을 줄이고, 분석 또는 시각화 성능을 향상시키는 데 주로 사용됩니다. 차원 축소는 데이터를 표현하는 데 필요한 특성 수를 줄이면서도 중요한 정보는 최대한 유지하려는 목표를 가지고 있습니다.
차원 축소는 특히 고차원 데이터(텍스트, 이미지, 시계열 데이터 등)를 다룰 때, 과적합 방지, 계산 효율성 향상, 시각화 등의 장점을 제공합니다.
주요 차원 축소 기법 및 수식 설명
1. PCA (Principal Component Analysis)
PCA는 데이터를 선형적으로 변환해 분산이 최대화되는 방향으로 차원을 축소하는 방법입니다.
- 목표: 데이터의 분산을 최대한 보존하면서 차원 축소.
- 수식:

- 여기서, X는 데이터 행렬, λ는 고유값, w는 주성분(고유벡터)입니다. 고유값 분해를 통해 분산이 가장 큰 방향(주성분)을 찾아 차원을 축소합니다.
- 사용 상황: 대규모 데이터에서 주된 패턴을 추출할 때, 데이터의 분산 구조를 이해하는 데 주로 사용됩니다.
2. t-SNE (t-Distributed Stochastic Neighbor Embedding)
t-SNE는 비선형 차원 축소 기법으로, 고차원의 데이터 포인트 간 인접 관계를 저차원에서도 유지하며 시각화하는 기법입니다.
- 목표: 고차원에서 가까운 데이터 포인트를 저차원에서도 가깝게 유지.
- 수식:

- 는 고차원에서의 두 점 간의 유사성 확률입니다. t-SNE는 고차원과 저차원에서 유사성을 유지하는 방식으로 KL 다이버전스를 최소화합니다.
- 사용 상황: 데이터의 복잡한 비선형 패턴을 시각화할 때, 특히 이미지나 텍스트 데이터에 적합.
3. UMAP (Uniform Manifold Approximation and Projection)
UMAP은 t-SNE와 유사한 비선형 차원 축소 기법으로, 고차원의 데이터 간 거리와 인접성을 저차원에서 보존합니다.
- 목표: 고차원에서 가까운 데이터를 저차원에서도 유지하며, 구조적 패턴을 보존.
- 수식:
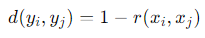
- 여기서 는 고차원에서의 데이터 간 관계를 나타내며, UMAP은 이를 저차원에서 거리로 변환해 클러스터 구조를 유지합니다.
- 사용 상황: 대규모 데이터에서 빠르고 확장 가능한 차원 축소 및 시각화에 적합.
4. LDA (Linear Discriminant Analysis)
LDA는 분류 작업에서 클래스 간의 분산을 최대화하면서 차원을 축소하는 지도 학습 기법입니다.
- 목표: 클래스 간 분산을 극대화하고, 클래스 내 분산을 최소화.
- 수식:
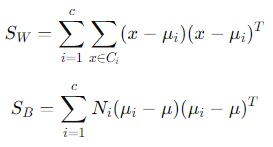
- 는 클래스 내 분산, SBS_B는 클래스 간 분산으로, 두 값을 최대화 및 최소화하는 방향으로 차원을 축소합니다.
- 사용 상황: 레이블이 있는 데이터에서 클래스 간 구분이 중요한 경우.
5. Autoencoder
Autoencoder는 신경망 기반의 차원 축소 기법으로, 입력 데이터를 압축한 후 다시 복원하는 과정을 통해 중요한 특징을 학습합니다.
- 목표: 고차원 데이터를 저차원으로 압축하면서 중요한 특징을 추출.
- 수식:

- 여기서 X는 입력 데이터, 는 복원된 데이터로, 원본과 복원된 데이터 간의 오차를 최소화하여 차원을 축소합니다.
- 사용 상황: 비선형 구조를 가진 데이터에서 효과적이며, 이미지나 텍스트 데이터에서 자주 사용됩니다.
6. Factor Analysis
Factor Analysis는 관측된 변수들을 몇 개의 잠재 요인으로 설명하여 차원을 축소하는 통계 기법입니다.
- 목표: 관측된 변수들을 잠재 변수들의 조합으로 표현.
- 수식:
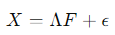
- 는 관측 변수, Λ는 로딩 행렬, F는 잠재 변수로, 잠재 변수의 선형 조합으로 데이터를 설명합니다.
- 사용 상황: 심리학, 사회과학 등에서 잠재 변수의 해석이 필요한 경우.
차원 축소의 필요성과 사용 상황
1. 고차원의 저주(Curse of Dimensionality):
고차원의 데이터는 차원 축소 없이 분석하거나 학습할 때, 과적합 또는 효율성 저하 문제를 겪기 쉽습니다. 차원 축소를 통해 이러한 문제를 해결하고, 데이터를 효율적으로 처리할 수 있습니다.
2. 시각화:
차원 축소는 2D 또는 3D 시각화를 통해 데이터의 군집화, 패턴 등을 확인할 수 있게 해줍니다. 특히 t-SNE나 UMAP은 복잡한 데이터의 구조적 관계를 시각화하는 데 매우 유용합니다.
3. 과적합 방지:
차원을 줄임으로써 모델이 불필요한 노이즈나 패턴을 학습하는 것을 방지하여, 모델의 일반화 성능을 높일 수 있습니다.
4. 계산 효율성 향상:
차원이 높은 데이터는 처리 비용이 매우 높아질 수 있지만, 차원 축소를 통해 계산 비용을 줄이고 모델 학습을 가속화할 수 있습니다.
결론
차원 축소는 고차원 데이터의 복잡성을 줄이고, 중요한 정보를 유지하면서도 효율적으로 데이터를 처리할 수 있게 해주는 중요한 기법입니다. 각 기법은 데이터의 특성에 맞춰 선택해야 하며, 이를 통해 과적합을 방지하고, 모델의 성능을 최적화할 수 있습니다.
'Data Science > machine learning' 카테고리의 다른 글
| LLM: 대규모 언어 모델의 원리, 종류, 그리고 활용 방법 (4) | 2024.09.28 |
|---|---|
| 딥러닝이란 (8) | 2024.09.28 |
| 클러스터링의 정의와 주요 방법들 (0) | 2024.09.28 |
| 분류(Classification)란? (2) | 2024.09.27 |
| 회귀(Regression)의 정의 (3) | 2024.09.27 |